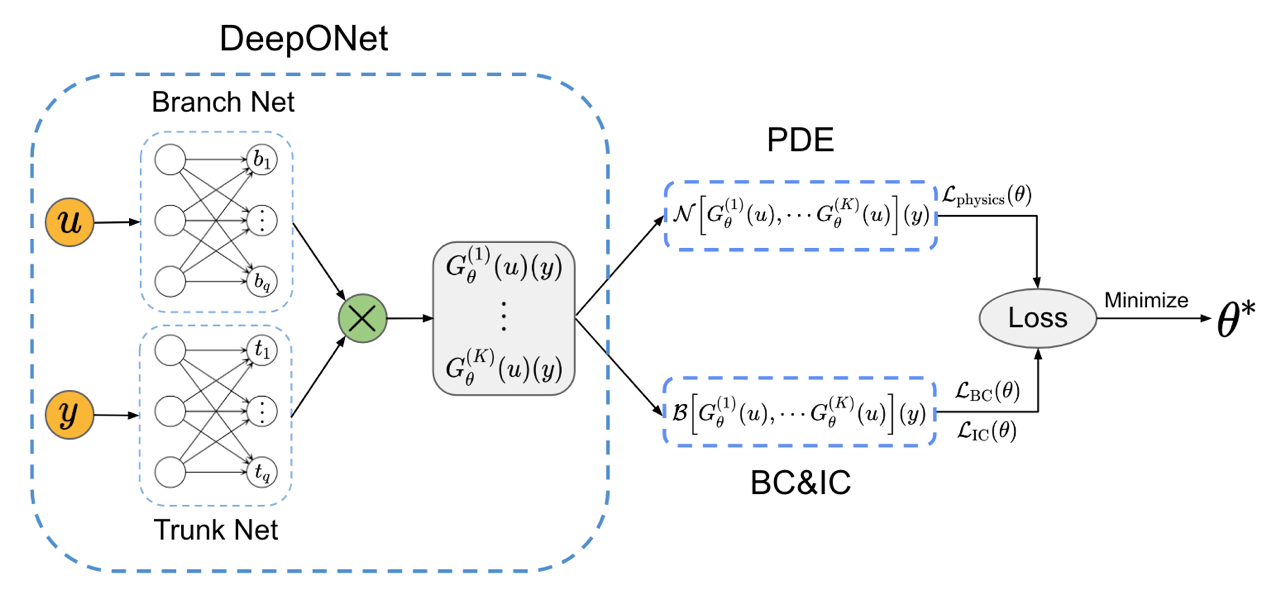
Physics-informed neural networks(PINNs)入门介绍
Physics-informed neural networks(PINNs)入门介绍
一、Introduction
PINNs定义:physics-informed neural networks – neural networks that are trained to solve supervised learning tasks while respecting any given laws of physics described by general nonlinear partial differential equations.
要介绍pinns,首先要说明它提出的背景。总的来说,pinns的提出是供科学研究服务的,它的根本目的是解方程,下面将以科学研究的发展史为主线引出pinns提出的背景条件,同时PINNs是data science方法
再次强调,PINNs方法本质是解方程!
中世纪以来,人类的科学研究发展史为:

划分间隔分别为1700以前的Empirical science时期,1700年到1950年的Theoretical science时期,还有1950年到2000年的computrational science时期以及现在处于的2000年后的Data science时期。
为了更深入地介绍这四个科学研究发展范式,下面将以流体问题的研究发展史的四个例子说明:
- Empirical science: 达芬奇用画稿描述流体流场
- Theoretical science: 用Navier-Stokes equation描述流程
- Computrational science: 用计算机求解Navier-Stokes equation
- Data science: 用PI-DeepONet求解Navier-Stokes equation
同时这四个例子也是为了引出下面几个名词定义:
- Theoretical science: PDE, ODE, 解析解, 微分方程f(t, x)范式
- Computrational science: 网格, 差分, 变分
- Data science: PINNs(PI)
Empirical science:
Leonardo da Vinci's scientific artistry led him to draw accurate patterns of eddies and vortices for various flow problems. 经验科学时期人们无法对观察到的现象进行量化而精确地描述,只能靠图册或者是语言描述大致的现象。

但是这一范式具有“量化问题”:达芬奇精美的画稿可以让人们比较清晰地理解流体流场的变化规律;这只能是一种经验上的总结,没有数值上的量化,不够精确;单纯的画稿无法囊括所有的流体问题,从画稿中想象流场在新的情景下的变化规律是不可靠的
对于其它科学问题的研究也面临相似的问题,因此需要一种新的研究范式可以更精确地量化各种实验现象
Theoretical science:
NavierStokes and continuity equations: \rho \frac{D V}{D t}=\rho f-\nabla p+\mu \nabla^{2} V
纳维-斯托克斯方程(Navier-Stokes equation)是描述粘性不可压缩流体动量守恒的运动方程,简称N-S方程。此方程是法国科学家C·L·M·H·纳维于1821年和英国物理学家G·G·斯托克斯于1845年分别建立的
但是这种范式同样有一个问题“求解问题”: 但是Navier-Stokes equation目前并没有解析解,只能靠“取巧”的方法求解,也就是数值计算方法求解
计算机技术的进步促进了数值计算方法的发展,可以帮助人们更快更精确地求解各类微分方程下面介绍各名词定义:
解析解:指符合某个微分方程和其初始条件及边界条件的
一个显式定义了自变量和因变量关系的函数
Example1-1:对于方程 u_{x}=\frac{1}{1+x^{2}} 其解析解为 u=\arctan x ,输入自变量得到对应因变量与解析解对应的,还有一种解为数值解 x=0.25\pi, u=\frac{\sqrt{2}}{2}; x=0, u=0; ...
微分方程:指定义了(自变量及其各阶微分)与因变量关系的函数关系式
Example2-1: u_{t}-0.0001 u_{x x}+5 u^{3}-5 u=0
一般地,把除 u_{t} 之外的 u 的各阶微分及其相互运算用非线性算子 \mathcal{N}[\cdot] 表示,并把方程所有项转移到左端,就能得到物理微分方程的一般通式 f(u, t):=u_{t}+\mathcal{N}[u], f(u, t)=0 该公式也可以被称为残差公式 u_{t} 即为 \frac{\partial u}{\partial t}
ODE:ODE(Ordinary differential equation)常微分方程;自变量只有一个的微分方程,一般描述物理现象的ODE系统一般都只含有t作为自变量
Example3-1: \frac{d s}{d t}=\cos (t)
PDE:PDE(Partial differential equation)偏微分方程;自变量多于一个的微分方程,一般描述物理现象的PDE系统一般都会含有t作为自变量,其余自变量更确切的含义是观察的维度
Example4-1:
Diffusion-reaction dynamics:
\begin{aligned} &\frac{\partial u}{\partial t}=D \frac{\partial^{2} u}{\partial x^{2}}+k u^{2}, \quad(x, t) \in(0,1] \times(0, T] \\ &u(x, 0)=u(x), \quad x \in[0,1] \\ &u(0, t)=u(1, t)=0, \quad t \in[0, T] \end{aligned}
1D wave equation:
\begin{aligned} &\frac{\partial^{2} u}{\partial t^{2}}=c^{2} \frac{\partial^{2} u}{\partial x^{2}}, \quad(x, t) \in[0,1] \times[0, T] \\ &u(0, t)=u(1, t)=0, \quad t \in[0, T] \\ &u(x, 0)=\sin (\pi x), \quad x \in[0,1] \\ &\frac{\partial u}{\partial t}(x, 0)=0 \end{aligned}
数值求解方法:
ODE
线性多步法:
Adams family
backward differentiation formula(BDF) family
线性单步法:Runge-Kutta methods
explicit Runge-Kutta
implicit Runge-Kutta
PDE
有限差分法
有限元法
Direct Method (Strong form)
Variational Method (Weak form)
Galerkin Method of Weighted Residuals (Weak form)
下面解释各名词定义:
有限差分法:
有限差分法是一种通过差分替代微分得到逼近原方程的离散形式的线性方程,再进行求解的微分方程求解方法
通常来说,将微分用差分近似表达的方式并不固定,eg:
\begin{aligned} & u_x=\lim _{\Delta x \rightarrow 0} \frac{u_{x}(x+\Delta x)-u}{\Delta x} \approx \frac{u(x+\Delta x)-u}{\Delta x} \\ & u_x=\lim _{\Delta x \rightarrow 0} \frac{u_{x}(x+0.5\Delta x)-u(x-0.5\Delta x)}{\Delta x} \approx \frac{u(x+0.5\Delta x)-u(x-o.5\Delta x)}{\Delta x} \end{aligned}
差分之后通常可以得到 \mathbf{A} \mathbf{u}=\mathbf{F} 或者是 \mathbf{A} \mathbf{u}=0 形式的线性方程,此时借此方程的唯一障碍就是矩阵求逆,可以用雅可比迭代等方法来完成
Example5-1:例如求解方程
\left\{\begin{array}{l} f(u, t)=u_{t}+\mathcal{N}[u] = u_t + u=0, \quad t \in[0, 1] \\ u(t=1)=0 \end{array}\right.
将其写成离散差分形式即为
\left\{\begin{array}{l} \left(u_{i+1}-u_{i}\right) / h + u_{i}=0 \\ u_{n}=0 \end{array} ; \quad i=1,2, \ldots, N-1\right.
这里有离散的结点表示 t_{i}=0+i h,(i=0,1,2,3,4) , 步长 h=(1-0) / N ,含义即为 t \in[0, 1] 上的离散化取点,也称为网格
一般的,上述差分形式也可在合并同类项后得到
u_{i+1}=\left(1-h c_{i}\right) u_{i}+h f_{i} ; u_{0}=d, i=0,1,2,3, \ldots, N-1
该递推公式可以写成矩阵形式
\left[\begin{array}{cccc} 1 & & & \\ 1 & 1 & & \\ & \ddots & \ddots & \\ & & 1 & 1 \end{array}\right]\left\{\begin{array}{c} u_{1} \\ u_{2} \\ \vdots \\ u_{N} \end{array}\right\}=-\left\{\begin{array}{c} u_{0} \\ 0 \\ \vdots \\ 0 \end{array}\right\}
该线性方程组可以用雅可比迭代求解逆矩阵最终得到各项 u_i
连续区间的离散化程度,或者说网格的精细程度越高,则 i 的个数越多,求解难度也越大
变分方法(Variational method):
变分指以函数作为变量
变分法的基本思想是将微分方程的对应解(或解析解)作为一个未知函数,以此为变量组建一个对应的积分形式的方程,通过求解新的方程获得微分方程的解
机器学习通过优化loss得到模型的思想和变分法的思想很接近


虚功原理的推导是从求解一根弦的位置平衡位置出发的,它通过构建平衡位置函数 u(x) 的等价极小位移公式(或者说最小势能),得到原平衡位置微分方程的等价变分形式,再推广到虚功原理描述的一般问题。
Strong form:直接描述问题
Weak form:用integral form描述问题
使用数值求解方法可以在保证一定精度的要求下求解微分方程
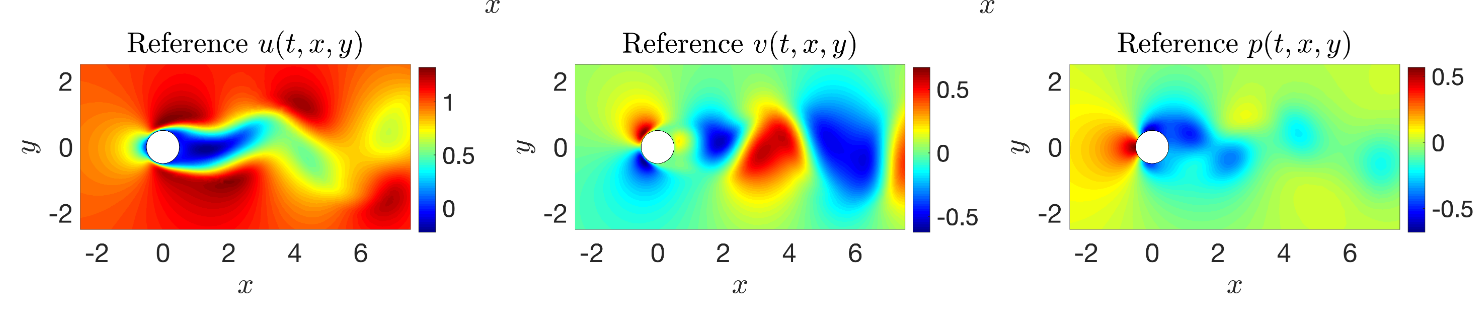
速度和精度问题:
数值方法求解微分方程可以得到较高的精度的结果,但是:各种高精度的数值方法普遍求解速度较慢;速度较快的数值方法求解精度不高;几乎所有数值方法都需要在事先设定网格上求解得到结果,无法自由地得到网格间的连续值
因此缺少一种能更快速求解的同时保持着较高求解精度的微分方程求解方法
为什么我们需要快速精确地求解微分方程:
这是由我们的实际科学研究需求决定的;现代科学研究需要emperiment, Theory, Computation者紧密结合

实验得到数据和理论计算结果进行对比验证; 通过实验结果总结理论并且反复修正完善;通过数值计算方法得到理论公式的计算结果
科学发展在这三者的循环迭代中不断得到发展,一旦某一个环节速度脱节就会影响整个迭代速度
数据科学可以辅助加速科学发展三要素(个人理解)的迭代循环:
Data science:
数据科学是将数据转化为决策和行动(tradecraft)的艺术,是人和计算机一起工作将数据转化为知识发现的工具、技术和流程的整合。数据学科通过收集数据、描述数据、发现知识,进而进行合理的有针对性的预测和建议。
机器学习方法,因为其强大的拟合非线性函数的能力而出名,诞生后就有人希望用其求解微分方程
不失一般性,往后Data science用Machine Learning替代
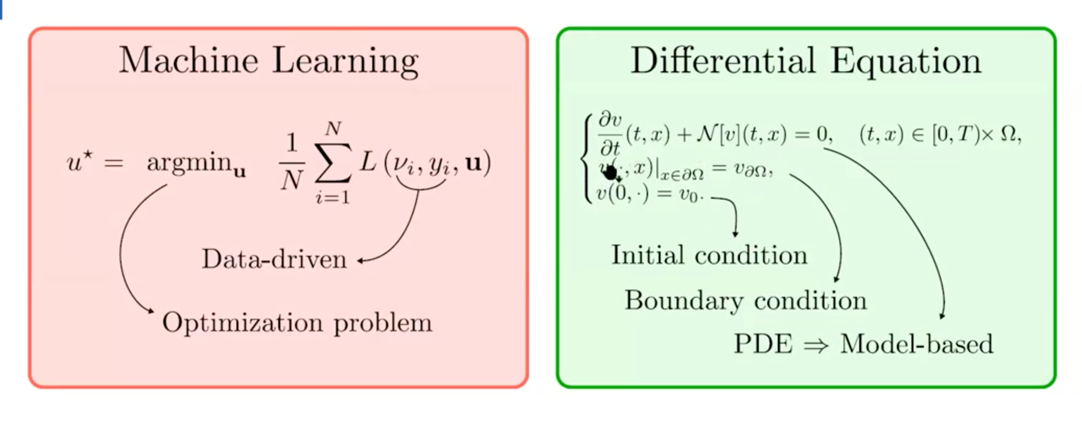
一个通用的微分方程一般由初始条件和边界值唯一确定,被确立时可以假设存在一个解。那么类比变分的思想,可以认为以该解作为变量输入微分方程中必定能被满足
机器学习模型通过优化损失函数使得在一定参数$u$下的网络不断逼近训练数据,其中的训练数据替代了微分方程的约束作用,损失函数就像变分法中微分方程的变分形式
回到最初的例子,即对于Navier-Stokes equations, 可以通过构建一个全连接的含有10层每层50个神经元的前馈神经网络来逼近方程解,一个有效的Navier-Stokes informed neural networks网络结构图如下
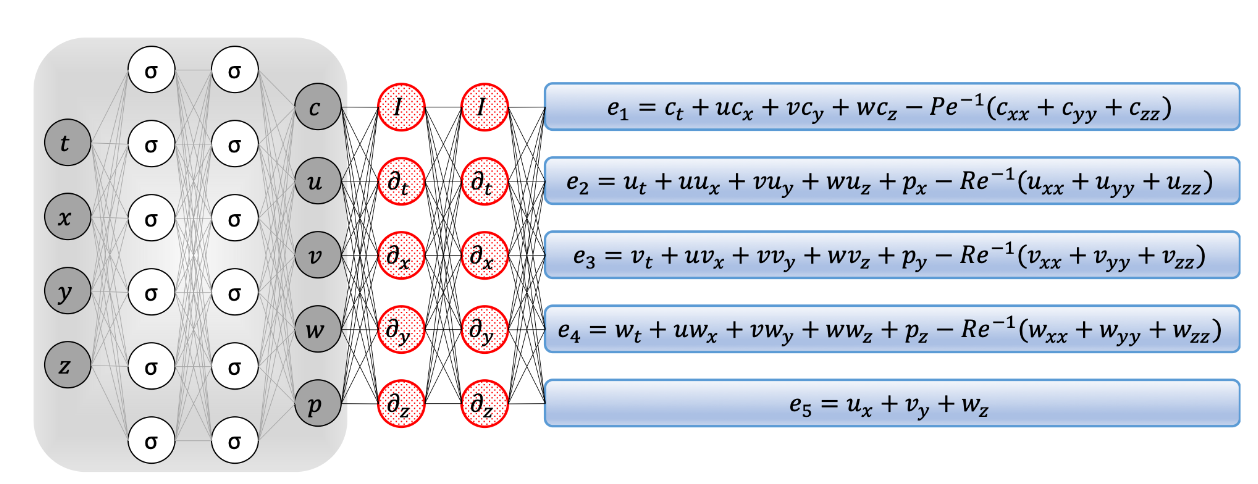
二、Physics-informed neural networks
最早期的神经网络求解微分方程方面的研究,是通过使用神经网络求解有限差分方程以此来求解微分方程问题
过了四年有人从变分法的出发将原用于逼近微分方程解的Galerkin Method改造成用神经网络来拟合
接着又有人提出用多层感知机求解(initial value and Boundary)微分方程(IBS),并与有限元中的Galekrkin方法比较
过了两年后,该作者在上一篇论文的基础上作出改进,讨论了如何求解复杂几何边界条件的问题
过了13年一篇博士论文提出了约束反向传播(CPROP)方法在训练过程中保留先验知识,将该方法推广到求解IBS问题的神经网络算法中得到约束积分方法
到了2018年,神经网络求解微分方程的研究迎来突破,DGM算法被提出,这是一种求解高维偏微分方程的无网格神经网络算法
同年,PINNs模型最早的提出者“Maziar Raissi”发表了论文介绍了研究如何从数据中学习隐含微分方程的工作
上面几篇论文为PINNs的提出奠定了良好的基础,特别是1994年和1998年的工作,PINNs的思想内核和它十分相近
1998:
所谓神经网络,不过是一个非线性函数逼近器。去求解非微分方程,在网络学习过程中不过是不断寻找适配微分方程的函数
1998年工作直接优化网络逼近解代入微分方程在各个离散点上的输出求和


1994:
该工作受变分原理启发,将变分方法Galerkin Method中的基函数换成神经网络,同时改造变分形式为更简单直接的形式以优化求解
该方法没有直接对积分形式进行离散化

截取1994年工作的核心公式
\int_{a}^{b} F R d x=(F, R)=0
\left(F, L\left(y_{a}\right)-g(x)\right)=0 \quad \text { or } \quad\left(F, L\left(y_{a}\right)\right)=(F, g)
观察可知其实该工作就是基于变分法的基本引理来完成的

1994年工作:Solution of Nonlinear Ordinary Differential Equations by Feedforward Neural Networks论文作者们
1998年工作解ODE:

1998年工作解PDE:

布朗大学教授“Maziar Raissi”;论文工作受美国 Darpa国防高级研究计划局资助;下属于Enabling Quantification of Uncertainty in Physical Systems(EQUiPS)物理系统不确定性量化

PINNs方法的核心思想可以用以下公式表达:
\begin{aligned} \theta^{\star}=\operatorname{argmin}_{\boldsymbol{\theta}} & \frac{1}{N} \sum_{i=1}^{N}\left(u_{\boldsymbol{\theta}}\left(t_{i}, x_{i}\right)-y_{i}\right)^{2} \\ \text { s. t. } & \frac{\partial u_{\boldsymbol{\theta}}}{\partial t}(t, x)+\mathcal{N}\left[u_{\boldsymbol{\theta}}\right](t, x)=0, \quad(t, x) \in[0, T) \times \Omega . \end{aligned}
再回顾变分法基本引理,可以得到:
\begin{aligned} \theta^{\star}=\operatorname{argmin}_{\boldsymbol{\theta}} & \frac{1}{N} \sum_{i=1}^{N}\left(u_{\boldsymbol{\theta}}\left(t_{i}, x_{i}\right)-y_{i}\right)^{2} \\ \text { s. t. } & \iint_{[0, T] \times \Omega}\left(\frac{\partial u_{\boldsymbol{\theta}}}{\partial t}(t, x)+\mathcal{N}\left[u_{\boldsymbol{\theta}}\right](t, x)\right)^{2} d t d x=0 \end{aligned}
上面公式的积分项目的是使残差公式几乎处处为零,同时使用最优化中的拉格朗日余项代替硬性约束得到:
\theta^{\star}=\operatorname{argmin}_{\theta} \frac{1}{N} \sum_{i=1}^{N}\left(u_{\theta}\left(t_{i}, x_{i}\right)-y_{i}\right)^{2}+\lambda \underbrace{\iint_{[0, T] \times \Omega}\left(\frac{\partial u_{\theta}}{\partial t}(t, x)+ \mathcal{N}\left[u_{\boldsymbol{\theta}}\right](t, x)\right)^{2} d t d x}_{\text {Physics cost }}
因为连续的积分不能简单计算,所以使用离散求和的方法计算积分:
\theta^{\star}=\operatorname{argmin}_{\boldsymbol{\theta}} \frac{1}{N} \sum_{i=1}^{N}\left(u_{\boldsymbol{\theta}}\left(t_{i}, x_{i}\right)-y_{i}\right)^{2}+\lambda \frac{1}{N_{\mathrm{phy}}} \sum_{j=1}^{N_{\mathrm{phy}}}\left(\frac{\partial u_{\boldsymbol{\theta}}}{\partial t}\left(t_{i}^{p}, x_{i}^{p}\right)+\mathcal{N}\left[u_{\boldsymbol{\theta}}\right]\left(t_{i}^{p}, x_{i}^{p}\right)\right)^{2}
PINNs方法同时融合了machine learning和differential equation,属于物理和数据同时驱动的一种神经网络方法:
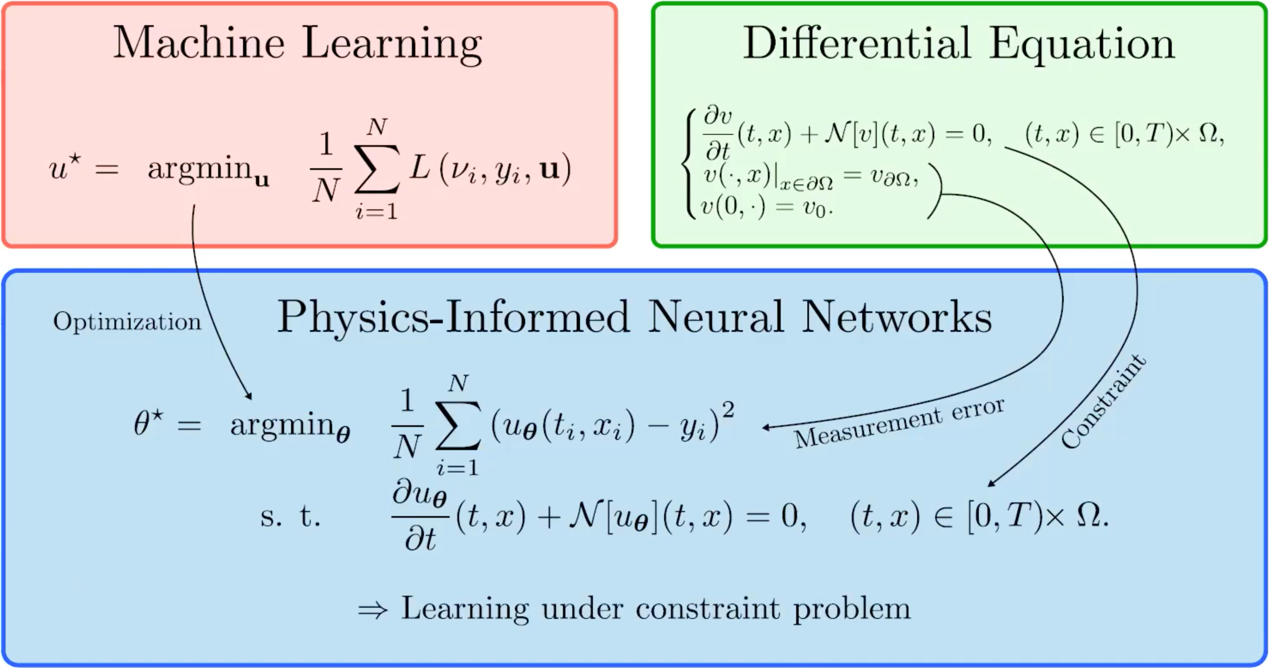
Example 6-1:
求解PDE方程
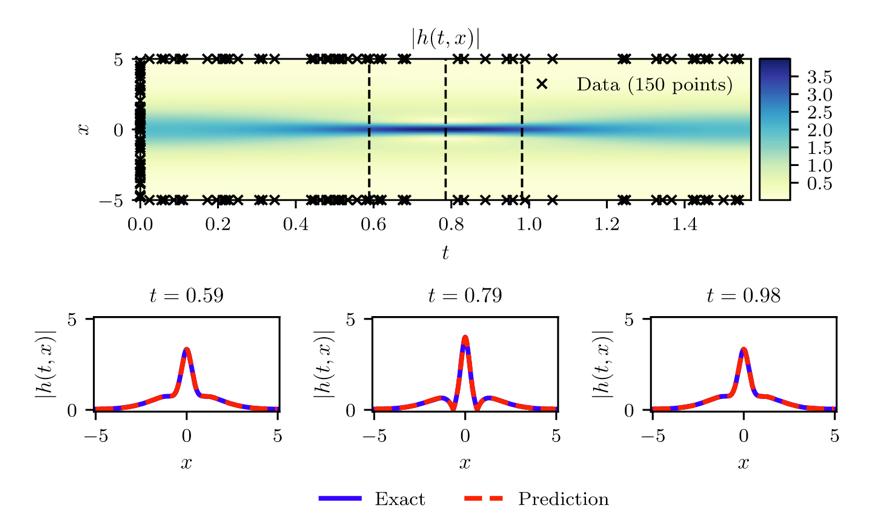
\begin{aligned} &i h_{t}+0.5 h_{x x}+|h|^{2} h=0, \quad x \in[-5,5], \quad t \in[0, \pi / 2] \\ &h(0, x)=2 \operatorname{sech}(x) \\ &h(t,-5)=h(t, 5) \\ &h_{x}(t,-5)=h_{x}(t, 5) \end{aligned}
有求解步骤大致如下所示:

Deepxde:DeepXDE is a library for scientific machine learning and physics-informed learning. 由Lulu博士组内开发,实现了大部分的PINNs和DeepONet以及multifidelity neural network算法
SimNet:Nvidia公司开发的基于PINNs方法的多物理场AI仿真工具包,主要用于热流仿真
NeuralPDE:a solver package which consists of neural network solvers for partial differential equations using scientific machine learning (SciML) techniques没有发现亮点的pinns求解包,貌似没有DeepONet方法
IDRLnet:由中国军事科学院黄创霞教授团队的Wei Peng博士组内开发,开发文档称框架受SimNet启发
三、Application
PINNs模型大致可以运用于三个area:
- forward problems,
- inverse problems,
- meta-PINN
forward problems:
直接求解没有任何标签数据的非显式微分方程
inverse problems:
求解带标签(有限数据)的含参数微分方程,并且得到参数的估计值
inverse problems example
- 可以类比在得到有限样本的情况下估计样本分布的问题
- 已知分布族下估计未知分布的分布参数可以类比于未知参数下的微分方程:
\begin{aligned} &u_{t}+\lambda_{1}\left(u u_{x}+v u_{y}\right)=-p_{x}+\lambda_{2}\left(u_{x x}+u_{y y}\right) \\ &v_{t}+\lambda_{1}\left(u v_{x}+v v_{y}\right)=-p_{y}+\lambda_{2}\left(v_{x x}+v_{y y}\right) \end{aligned} 和 f(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}
meta-PINN:
- 原始的PINNs一般一次训练只能求解固定初始值下的微分方程,即 \{t_{0}, \mathbf{x_{0}}, \mathbf{u_{0}}\} 变化时,必须要重新训练。同时从一组初始值下训练的PINNs也不能直接迁移到其它初值值条件下的任务开始训练。
- 理想的一种微分方程求解方法应该是能够计算大部分初值条件下的微分方程,每次都要重新训练是不现实的。
- 应该要寻求一个元学习方法,可以在训练时在含有多个初值条件设定下的数据集下训练,测试时也能在多个初值条件设定下的数据集下测试
应用:
- 求解1D ALelen-Cahn equation

- 求解1D Schrodinger equation
- 英伟达设计simnet把PINNs用于优化结构设计,主要目的是优化散热

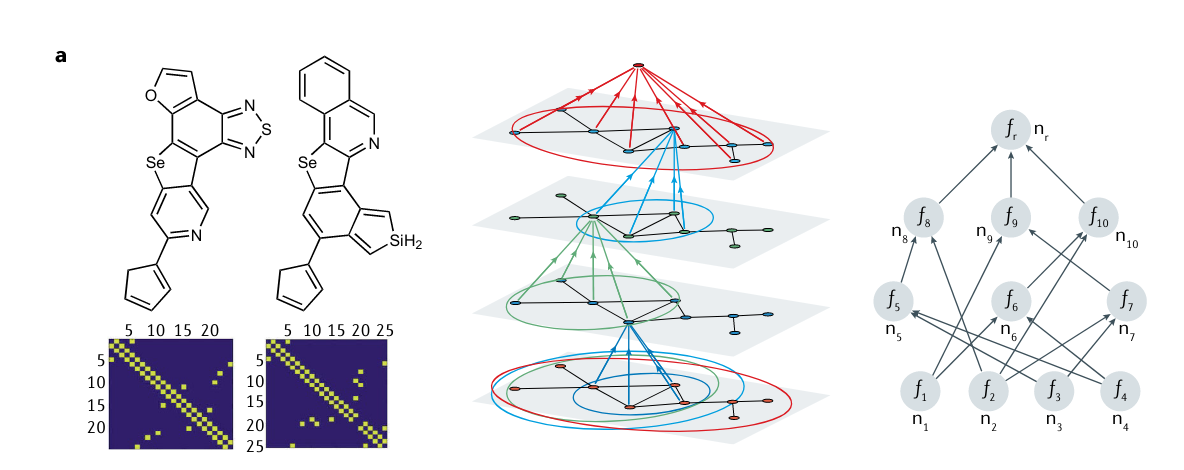
- 可以使用PINNs预测分子性质
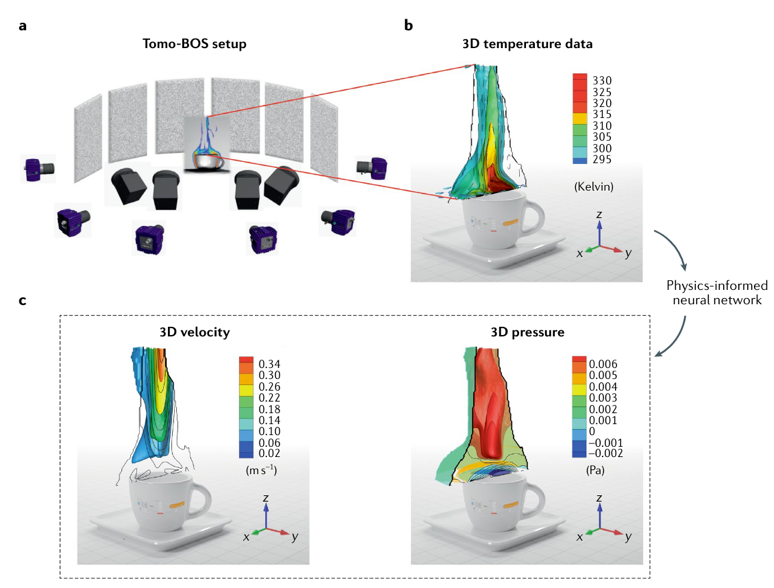
- 可以使用PINNs结合成像系统预测咖啡杯上流体的3D流动
- PINNs可以用于去噪和重建临床磁共振成像(MRI)的血流速度数据,下图是猪主动脉血流的活体4D流磁共振成像用PINNs处理后的结果

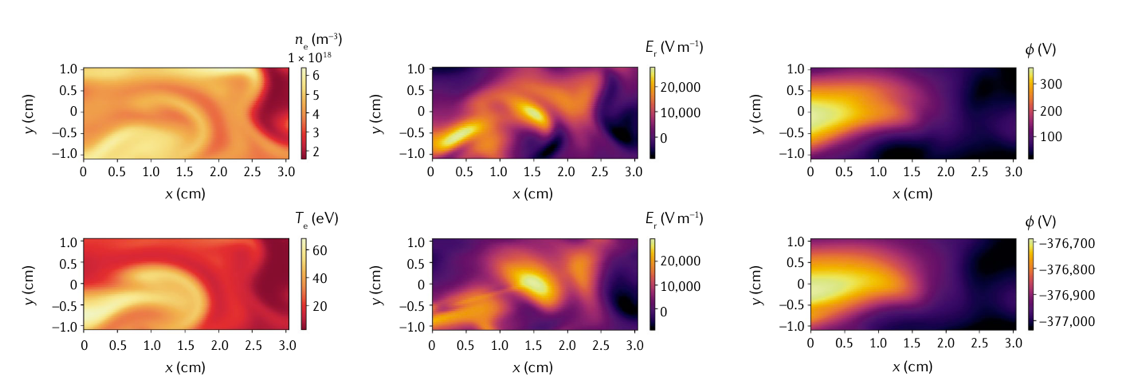
- PINNs还可以用于模拟等离子体动力学,特别是比较受关注的磁约束聚变的边缘等离子体行为。下图展示的是3D磁化双流体模型的预测比较结果(下面一行是PINNs预测值)
- 其它应用:quantum chemistry;material sciences;molecular simulations;geophysics
目前解决meta-PINN问题最有效的模型是PI-DeepONet模型