扒一扒那些叫欧拉的定理们（一）——基本介绍和简单多面体欧拉定理

欧拉印象

欧拉（Leonhard Euler），1707-1783，主要数学贡献领域在微积分和图论上，比如我们初中就在学校学的函数的记法f(x)，就是由欧拉首先引入的。因为数学的基础作用，他的研究成果也延伸到力学，光学，天文学等各个领域。

欧拉是18世纪杰出的数学家，同时也是有史以来最伟大的数学家之一。他也是一位多产作者，其学术著作有60-80册。法国数学家皮埃尔-西蒙·拉普拉斯曾这样评价欧拉对于数学的贡献：“读欧拉的著作吧，在任何意义上，他都是我们的大师”。

相信大家在从小的数学学习经历中，都或多或少地学习过他给人类留下的智慧。他对人类数学的贡献无处不在，但估计我穷尽一生，也难以完全了解其全貌。这些贡献从数学发端，又以数学模型的形式延展到物理学，天文学，经济学等各个领域，简直是数学全才的标准模板，和高斯一同组成了闪耀在18世纪天穹上的双子星。

写作动机

近日，不断在各个地方，或偶然或必然地学习到或回顾到他的成就，尤其是一种叫“欧拉定理”的神奇定理，竟然涵盖了几何，图论，拓扑，数论，经济学等这么多领域。我想，著作等身应该还不够形容他的伟大，发表的定理自己的名字不够命名用，这才是真的凡尔赛吧！

不你知道你印象中的欧拉定理是哪一个？远在还在念小学时，在给我数学启蒙的《数学的奥秘》一书中，第一次见到了欧拉定理，大概是讲的在空间中多面体的点线面数量一系列加减以后结果为2的一个公式，是我众多数学美的记忆之一；后来，在奥数课里的平面几何讲到过欧拉定理，现在回忆起来也满满的平面几何定理巅峰级别的智慧；上大学以后在在傅里叶级数和复变函数等课程里反复地玩转着欧拉公式，并在电路分析中找到了其描述交流电周期性的物理意义；旁听经济学课的时候，没想到这家伙居然在宏观经济学上也没忘了留下自己的足迹。毕业以后，没忘了对数学的热爱，又发现了欧拉几何定理的图论描述以及以示性函数表示的拓扑不变量。最后还补课了数论中的欧拉定理，并发现在群论中，这是一个多么直白的结论。

回看这一切我才发现，这么多年的数学求学生涯里，我一直浸润在大师的智慧下，这是多么的幸运。不断地学习到各种欧拉定理，欧拉公式，更别提还有好多欧拉解决的问题，比如小学图论入门的柯尼斯堡七桥问题等等，真的有一种乔丹霸榜NBA历史各个数据榜单的老流氓一样的感觉，怎么哪都有你？大胆揣测一下，可能这就是降维打击吧，高一个级别的智慧在各个领域用起来，都是通用并吊打的。

学识水平有限，我无法穷尽先生所有的成就，仅就我目力所及的叫“欧拉定理”的内容，伴随着众多领域中出现的，叫欧拉的公式，给大家分享一下作为一个数学爱好者的感受。希望能够给大家提供一个理解这些智慧的视角，也是对自己这些内容学习的总结。大体内容包括：

1. 简单多面体欧拉定理及图论和高维空间的抽象形式

2. 平面几何欧拉定理及其相关性质

3. 欧拉复指数公式

4. 欧拉数论定理

5. 欧拉经济学定理

这里的每个章节都是数学史和现代数学学习中了不得的成就和内容，借由欧拉先生的研究，把它们串在了一起，写每个章节时我也是一边写，一边翻阅了大量的资料，希望能对读者的数学学习有所裨益。

简单多面体欧拉定理简介

今天我们先进入整个系列的第一个部分：简单多面体欧拉定理。很多孩子学习的第一个神奇的立体几何定理，恐怕就是这个又简单又迷人深邃的结论吧！

数学的发现有时候是从具体对象中抽象出来的模型，比如以牛顿三定律需要的计算为背景发明的牛顿莱布尼兹公式，有的就直接在数学范畴内玩了，纯的数论定理像哥德巴赫猜想，费马大定理等都是如此。我认为最美的那类数学结论能够兼顾这两个方面，既能在纯数学领域内有足够深刻的抽象，又能够作为足够简单明了的现实对象的模型的例子。横跨立体几何，图论和拓扑学的欧拉定理就是这种极具观赏性的数学定理，接下来就让我们一起见证这数学奇迹吧！

简单多面体欧拉定理：对于简单多面体，其各维对象数总满足一定的数学关系，在三维空间中设其顶点，边和面的数量分别为V, E, F，则欧拉定理可表示为：

V - E + F = 2

这个公式也称为（立体几何）欧拉公式，其简洁精炼的程度恐怕也只有他自己的复数欧拉公式和爱因斯坦质能方程能与之媲美了吧！这公式的结论长得简直就像魔术的奇迹一样，随便拿个西瓜，把所有的皮都用刀切掉，就这么一个随意的简单多面体，其顶点，边，面的数量，居然有着这样的恒等关系！

不，还没完，当你尝试分析这内部的结构并试着证明它，发现它的奥秘时，这探索过程简直比魔法呈现的表象还要美！

从简单多边形到简单多面体

为了数学严谨，我们先来介绍一下简单多面体，它是一类特殊的多面体，满足以下条件：

(1) 各面都是简单多边形；

(2) 多面体的棱彼此之间、棱与面的内部都没有公共点；

(3) 多面体的各顶点不附着于各面的内部或各棱之上；

(4) 多面体上共有一顶的一切面角，围拱着这个顶只构成一个多面角。

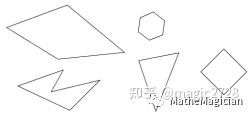
看起来有点多和复杂，那我们先看二维的简单情况，简单多边形。所谓简单多边形，定义为由直线，非相交的线段或“边”组成的扁平形状，其成对连接以形成封闭路径。这概念属于典型的一说定义就懵但是拿出具体实例来有好像明白的类型，大家理解“简单”其实大体就指的任意两边不相交，而平常我们说的多边形，也常常省略“简单”二字。用图论的话讲其实就是一个平面内点集的循环线段序列（圈），且要求所有相邻关系对应的线段两两不相交。其实直观上也很好判断，只要每条边都是直的，互相不相交，就行了。分类上，根据是否任意两点连线都在多边形内，分为凸多边形和凹多边形两种。以下这些图都是简单多边形：图1 简单多边形

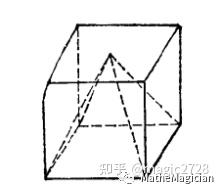
有了简单多边形的概念，简单多面体就好理解多了。比如下面这个图就不是简单多面体，因为它凹进去那个顶点附着在了一个面上。图2 非简单多面体

显然你完整地一刀刀切下去也切不出这样的西瓜块，而其它的无论如何歪七扭八的多面体，一般都是简单多面体了，比如：图3 简单多面体

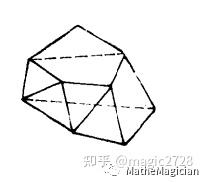
图4 简单多面体

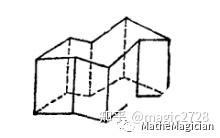
注意，我们常说的凸多面体（也叫欧拉多面体），一定是简单多面体，但是它还要求其整个多面体都在其每个面的同一侧，这样，至少要每个面都得是凸多边形，而且，不能有向内挖空的生成面，比如图2如果凹进去的顶点没有在顶面上，也不是凸多面体，但是是简单多面体；图3是个凸多面体，图4则因为顶底面都是凹多边形，所以也不是凸多面体，只是简单多面体。欧拉定理有时候陈述为对凸多面体的性质，但是其实对简单多面体也是成立的。

好了，我们从直观上和严格的数学定义上都聊清楚了简单多面体欧拉定理的内容，那这个定理到底该怎么证明，我们从证明中又可以学习到什么呢？下期精彩继续！

更多精彩内容，欢迎扫码关注公众号MatheMagician.