Harmonic Generation in Optical Vortex Fields

Abstract

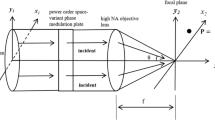
In this work the interaction of a thin medium of neon gas localized in the focal region of sharply and loosely focused Gaussian, radially, and azimuthally polarized fields is investigated. The distribution of fields in the focal plane is described using the Richards–Wolf theory, taking into account the presence of three spatial field components in the solution. The generated harmonics are investigated from the point of view of the intensity and polarization state described within the framework of the 3D Stokes parameters formalism. The results are studied in dependence on the distance from the focal plane to the detector, as well as their distribution in the plane perpendicular to the optical axis. The efficiency of harmonic generation in different spatial modes is investigated, as well as the topology of the spatial distribution of individual harmonics in the plane perpendicular to the optical axis.

Appendices

Appendix A

INTEGRALS THAT ENTER THE RICHARDS–WOLF SOLUTION FOR A FIELD IN DIFFERENT SPATIAL CONFIGURATIONS

In the formulas for the fields in the lens focus, according to the Richards–Wolf solution [14] (similar results may be obtained within the vector theory of Debye focusing [15]), we introduce the denotations for the integrals listed below:

$$I_{00}=\int\limits_{0}^{\theta_{\text{max}}}f_{w}(\theta)(\cos\theta)^{1/2}\sin\theta(1+\cos\theta)$$

$${}\times J_{0}(k\rho\sin\theta)\exp^{\imath kz\cos\theta}d\theta,$$

(22)

$$I_{01}=\int\limits_{0}^{\theta_{\text{max}}}f_{w}(\theta)(\cos\theta)^{1/2}\sin^{2}\theta J_{1}(k\rho\sin\theta)$$

$${}\times\exp^{\imath kz\cos\theta}d\theta,$$

(23)

$$I_{02}=\int\limits_{0}^{\theta_{\text{max}}}f_{w}(\theta)(\cos\theta)^{1/2}\sin\theta(1-\cos\theta)$$

$${}\times J_{2}(k\rho\sin\theta)\exp^{\imath kz\cos\theta}d\theta,$$

(24)

$$I_{10}=\int\limits_{0}^{\theta_{\text{max}}}f_{w}(\theta)(\cos\theta)^{1/2}\sin^{3}\theta J_{0}(k\rho\sin\theta)$$

$${}\times\exp^{\imath kz\cos\theta}d\theta,$$

(25)

$$I_{11}=\int\limits_{0}^{\theta_{\text{max}}}f_{w}(\theta)(\cos\theta)^{1/2}\sin^{2}\theta(1+3\cos\theta)$$

$${}\times J_{1}(k\rho\sin\theta)\exp^{\imath kz\cos\theta}d\theta,$$

(26)

$$I_{12}=\int\limits_{0}^{\theta_{\text{max}}}f_{w}(\theta)(\cos\theta)^{1/2}\sin^{2}\theta(1-\cos\theta)$$

$${}\times J_{1}(k\rho\sin\theta)\exp^{\imath kz\cos\theta}d\theta,$$

(27)

$$I_{13}=\int\limits_{0}^{\theta_{\text{max}}}f_{w}(\theta)(\cos\theta)^{1/2}\sin^{3}\theta J_{2}(k\rho\sin\theta)$$

$${}\times\exp^{\imath kz\cos\theta}d\theta,$$

(28)

$$I_{14}=\int\limits_{0}^{\theta_{\text{max}}}f_{w}(\theta)(\cos\theta)^{1/2}\sin^{2}\theta(1-\cos\theta)$$

$${}\times J_{3}(k\rho\sin\theta)\exp^{\imath kz\cos\theta}d\theta.$$

(29)

Fig. 8

Richards–Wolf solutions for the principal Gaussian mode $HG_{00}$. The upper row is for the case of sharp focusing, $f_{0}=1$, the lower row is for the case of weak focusing, $f_{0}=0.1$; (a, d) $x$ component, (b, e) $y$ component, and (c, f) $z$ component.

Fig. 9

Richards–Wolf solutions for the radially polarized mode. The upper row is for the case of sharp focusing, $f_{0}=1$, the lower row is for the case of weak focusing, $f_{0}=0.1$; (a, d) $x$ component, (b, e) $y$ component, and (c, f) $z$ component.

Fig. 10

Richards–Wolf solutions for the azimuthally polarized mode. The upper row is for the case of sharp focusing, $f_{0}=1$, the lower row is for the case of weak focusing, $f_{0}=0.1$; (a, d) $x$ component, (b, e) $y$ component, and (c, f) $z$ component.

Appendix B

ILLUSTRATION OF THE RICHARDS–WOLF SOLUTIONS FOR DIFFERENT FIELD MODES

We orient the $z$ axis along the direction of the incident light propagation along the axis of symmetry of the focusing system. The incident field is oriented along the $x$ axis. In Fig. 8 we present the Richards–Wolf solution for the module of electric field of the principal Gaussian mode in the case of sharp and weak focusing; Fig. 9, for the radial mode, and Fig. 10, for the azimuthal mode.

Fig. 11

The squares of modules of sublevel populations averaged over the time of pulse passage with different $m$ in dependence on the focusing sharpness for the principal Gaussian mode $HG_{00}$. The upper row is for the case of sharp focusing, $f_{0}=1$, the lower row is for the case of weak focusing, $f_{0}=0.1$; (a, d) $m=-1$, (b, e) $m=0$, and (c, f) $m=1$.

Fig. 12

The squares of modules of sublevel populations averaged over the time of pulse passage with different $m$ in dependence on the focusing sharpness for the radial mode. The upper row is for the case of sharp focusing, $f_{0}=1$, the lower row is for the case of weak focusing, $f_{0}=0.1$; (a) $m=-1$, (b) $m=0$, and (c) $m=1$.

Fig. 13

The squares of modules of sublevel populations averaged over the time of pulse passage with different $m$ in dependence on the focusing sharpness for the azimuthal mode. The upper row is for the case of sharp focusing, $f_{0}=1$, the lower row is for the case of weak focusing, $f_{0}=0.1$; (a, d) $m=-1$, (b, e) $m=0$, and (c, f) $m=1$.

Appendix C

SOLUTION TO THE SYSTEM OF DIFFERENTIAL EQUATIONS FOR POPULATIONS OF SUBLEVELS WITH DIFFERENT $m$ IN DEPENDENCE ON FOCUSING

In Fig. 11 we show the squares of modules of the sublevel populations averaged over the time of pulse passage (the wavelength of 800 nm and duration of 30 fs) with different $m$ in dependence on the focusing sharpness for the principal Gaussian mode; Fig. 12, for the radial mode, and Fig. 13, for the azimuthal one.